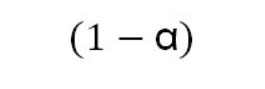
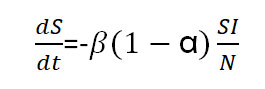
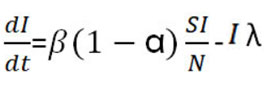
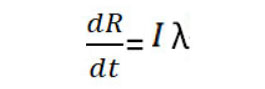

میتوانیم با اعمال محدویتهای اجتماعی ماگزیمیم بیماری را کنترل و باعت از بینرفتن اپیدمی با کمترین هزینه شویم
امروز میخواهم به بیماری کرونا که یکی از اصلیترین مسئلههای مهم دنیا و زندگی شخصی و اجتماعی شده بپردازیم البته نه از دیدگاه پزشکی و گسترش بیماریهای اپیدمی بلکه از دیدگاه ریاضیات و با زبان بسیار بسیار ساده. لازم است یادآوری کنم در این مقاله تنها از سادهترین مدل معتبر که برای همگان قابل درک است استفاده شده.
همانطور که میدانید بشر در طول تاریخی مدنی خود شاهد بیماریهای اپیدمی مختلفی بوده که بدترین آنها آنفولانزای اسپانیایی در سال 1918 بود که منجر به مرگ 50 میلیون شد. لازم به یادآوریست که همه اپیدمیها سرانجام پایانپذیر هستند و نمیتوانند برای همیشه باقی بمانند و ما مهمترین نقشی که میتوانیم در این میان داشته باشیم کاستن از خسارتهای جانی و اقتصادی است که برای این امر، شناخت نحوه گسترش بیماری و راههای مهار آن نقش کلیدی و اساسی را بازی میکند. برای این منظور شاخههایی از علم ریاضیات به بررسی مدلهای ریاضی بیماریهای اپیدمیک و پیامدها و نحوههای کنترل این بیماریها میپردازد و سعی میکند که اهمیت ساختارهای زیربنایی چون خدمات بیمارستانی و چگونگی برخورد منطقی این مشکل را به همه از جمله حاکمان یادآوری کند. برای ساده شدن درک موضوع را با موضوعات پایهای شروع میکنیم.
همانطور که میدانید بشر در طول تاریخی مدنی خود شاهد بیماریهای اپیدمی مختلفی بوده که بدترین آنها آنفولانزای اسپانیایی در سال 1918 بود که منجر به مرگ 50 میلیون شد. لازم به یادآوریست که همه اپیدمیها سرانجام پایانپذیر هستند و نمیتوانند برای همیشه باقی بمانند و ما مهمترین نقشی که میتوانیم در این میان داشته باشیم کاستن از خسارتهای جانی و اقتصادی است که برای این امر، شناخت نحوه گسترش بیماری و راههای مهار آن نقش کلیدی و اساسی را بازی میکند. برای این منظور شاخههایی از علم ریاضیات به بررسی مدلهای ریاضی بیماریهای اپیدمیک و پیامدها و نحوههای کنترل این بیماریها میپردازد و سعی میکند که اهمیت ساختارهای زیربنایی چون خدمات بیمارستانی و چگونگی برخورد منطقی این مشکل را به همه از جمله حاکمان یادآوری کند. برای ساده شدن درک موضوع را با موضوعات پایهای شروع میکنیم.
اگر یک بیماری در جامعهای باشد، با فرض منتفی بودن مسافرت، میتوانیم یک فرمول بسیار ساده از کل افراد جامعه با توجه به شرایط بیماری را به این شکل بنویسم: اگر N را کل جمعیت؛ S را جمعیتی که میتوانند بیماری را بگیرند؛ I را جمعیت بیمار؛ R را جمعیت بهبود یافته و یا فوت شده نامگذاری کنیم، آنگاه به رابطه ساده زیر میرسیم:
N=S+I+R
در گسترش بیماری، سرعت واگیری β و میزان سرعت درمان بعلاوه فوت را λ فرض میکنیم. این مقادیر عوامل تعیین کننده مهمی در این مدل هستند. هر بیماری بر حسب نوع بیماری، میزان سرعت همهگیری خاص خود را دارد، ظاهرا این پارامتر در ویروس کرونا عدد بزرگی است، به دو علت مهم خاصیت بیولوژیکی ماندگاری ویروس در محیط و همچنین طولانی بودن دوره نهفته این بیماری. از طرفی دیگر میتوان این مقادیر را با اعمال محدودیتهای اجتماعی و قرنطینه کنترل کرد برای این منظور به راحتی میتوانیم فرمول اجرای محدویتها را به شکل زیر بنویسیم:
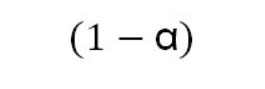
α=1 به معنی بسته بودن همه جا از جمله فروشگاههای مواد غذایی و پمپ بنزین و ایجاد محدویتهای رفتوآمد شهری را در نظر میگیریم؛ و α=0 یعنی هیچ محدودیتی برای کسی ایجاد نشود.
حال معادله دیفرانسیلی که دینامیک هر کدام از جمعیتها را بیان میکند را میتوانیم تشکیل دهیم:
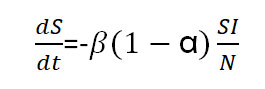
که در آن میزان تغییرات افراد در معرض مستعد تماس با زیاد شدن تماس با بیماران کاهش پیدا کرده به جمعیت بیمار اضافه میشود. همانطور که میبینید با اعمال سختگیری قرنطینه افراد سالم کم نخواهند شد. و اما برای محاسبه افراد سالم خواهیم داشت:
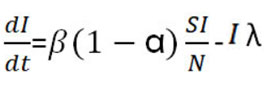
بدین ترتیب طبق فرمول بالا مبتلا شدن باعت افزایش جمعیت مبتلایان شده، همچنین میزان بهبودیافتهها و فوتیها نیز از جمعیت بیماران خواهد کاست. همانطور که مشخص است، سیاست سختگیری قرنطینه باعت کاهش مبتلایان جدید میشود. اما معادله زیر نیز معادله بهبود خواهد بود:
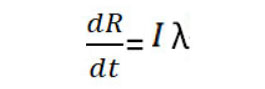
بدین ترتیب میزان رشد بهبودی و یا فوت محاسبه خواهد شد.
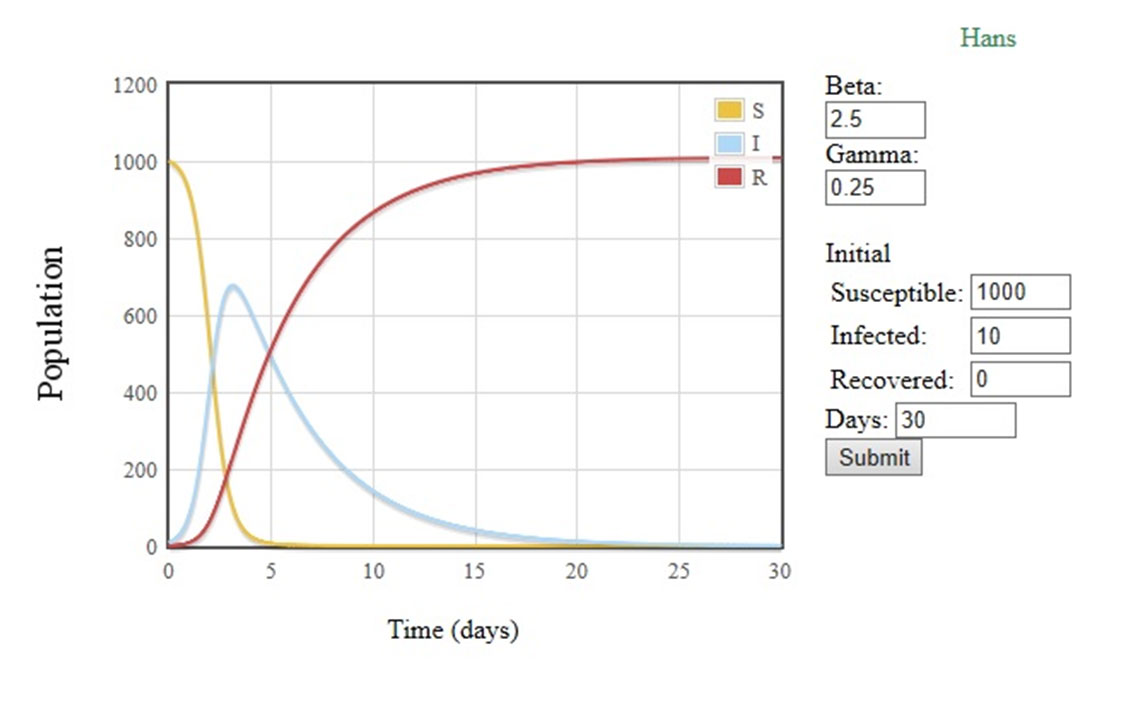
حال میخواهیم مدل ریاضی را خود با استفاده از تکنیکهای عددی حل و نتایج شبیهسازی شده را با توجه به گرافهای خروجی آنالیز کنیم. با معادلات بالا و بدون در نظر گرفتن هیچگونه محدودیت اجتماعی به منحنی زیر میرسیم:
حال میخواهیم مدل ریاضی را خود با استفاده از تکنیکهای عددی حل و نتایج شبیهسازی شده را با توجه به گرافهای خروجی آنالیز کنیم. با معادلات بالا و بدون در نظر گرفتن هیچگونه محدودیت اجتماعی به منحنی زیر میرسیم:

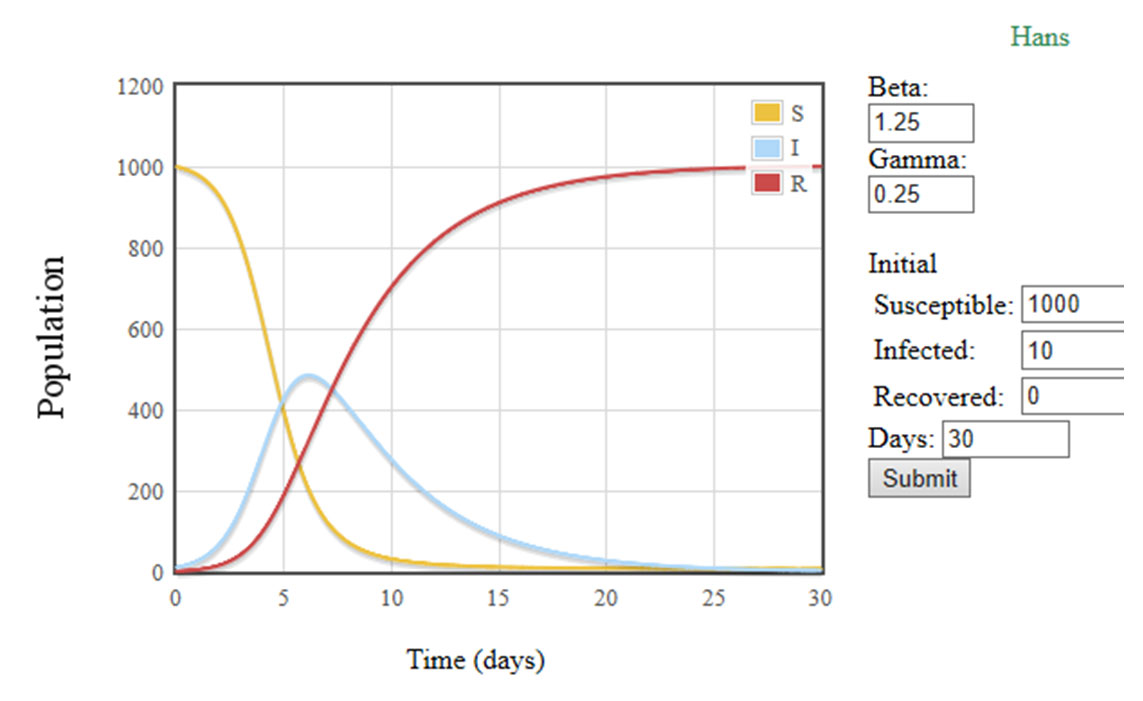
بسیار خوب، حال اگر بخواهیم این منحنی را با اعمال 50 درصدی محدودیت اجتماعی، بررسی کنیم منحنی به شکل زیر درخواهد آمد و مشاهده میکنید که منحنی I یا جمعیت بیمار نسبت به قبلی هم پهنتر میشود و هم از بلندی آن کاسته میگردد:

و اگر محدودیت اجتماعی 75 درصدی را اعمال کنیم همین منحنی آبی جمعیت بیمار بسیار پهنتر و از بلندی کوتاهتر خواهد شد:

نتیجهگیری: اگر فرض کنیم جمعیت شهر 1000 نفر بوده و هر نفر بتواند در طی 4 روز بیماری را به 10 نفر منتقل کند، میتوانیم با اعمال محدویتهای اجتماعی ماگزیمیم بیماری را کنترل و باعت از بینرفتن اپیدمی با کمترین هزینه شویم. از طرف دیگر محدودیت امکانات بیمارستانی و توانایی یک شهر در ارایه خدمات درمانی نیز از دیگر پارامترهای مهم در این شرایط ویژه میباشد.
همانطور که می بینید در گراف اول یعنی زمانی که محدودیتی در نظر گرفته نشده، تعداد بیماران در حالت ماگزیمم حدود 700 نفر و زمان رسیدن به این نقطه حدودا 6 روز بوده؛ درصورتی که با اعمال 50 درصد محدودیت تعداد ماگزیمم به کمتر از 500 نفر کاهش و زمان رسیدن به 8 روز افزایش پیدا کرده؛ و در نمودار آخر اعمال 75 درصدی محدودیت اجتماعی تعداد مگزیمم را به زیر 200 نفر و زمان رسیدن به این نقطه را به حدود 12 روز افزایش دادهایم.
در این مطلب تلاش کردیم با استفاده از علم ریاضی به اهمیت اعمال محدودیتهای اجتماعی بپردازیم و اینکه تکتک افراد چگونه میتوانند در کنترل این بیماری و این معضل جهانی کمک کنند. پارامترهای بکار گرفته در این مدلسازی بر اساس تخمین بوده و میتوانند صددرصد واقعی نباشند ولی بگونهای محاسبه شدهاند که بطور صحیح و زبانی ساده گویای شرایط اپیدمی باشند. بنابراین ایجاد محدودیتهای اعلان شده در تماس بین افراد اصلیترین نقش را در کنترل یک بیماری اپیدمی دارد.
همانطور که می بینید در گراف اول یعنی زمانی که محدودیتی در نظر گرفته نشده، تعداد بیماران در حالت ماگزیمم حدود 700 نفر و زمان رسیدن به این نقطه حدودا 6 روز بوده؛ درصورتی که با اعمال 50 درصد محدودیت تعداد ماگزیمم به کمتر از 500 نفر کاهش و زمان رسیدن به 8 روز افزایش پیدا کرده؛ و در نمودار آخر اعمال 75 درصدی محدودیت اجتماعی تعداد مگزیمم را به زیر 200 نفر و زمان رسیدن به این نقطه را به حدود 12 روز افزایش دادهایم.
در این مطلب تلاش کردیم با استفاده از علم ریاضی به اهمیت اعمال محدودیتهای اجتماعی بپردازیم و اینکه تکتک افراد چگونه میتوانند در کنترل این بیماری و این معضل جهانی کمک کنند. پارامترهای بکار گرفته در این مدلسازی بر اساس تخمین بوده و میتوانند صددرصد واقعی نباشند ولی بگونهای محاسبه شدهاند که بطور صحیح و زبانی ساده گویای شرایط اپیدمی باشند. بنابراین ایجاد محدودیتهای اعلان شده در تماس بین افراد اصلیترین نقش را در کنترل یک بیماری اپیدمی دارد.
اگر شما همکاری گرامی ما هستی، مرسی که این مطلب را خواندی، اما کپی نکن و با تغییر به نام خودت نزن، خودت زحمت بکش!
پروتکل علمی - پزشکی جهانی برای مقابله کلیه ویروسهایی مانند کرونا که انتقالشان از طریق بسته هوایی است:
۱- ماسک ان-۹۵ بزنید، کرونا از ماسکهای معمولی رد میشود. ۲- فیلتر هوای قوی هپا بگذارید. ۳- تا جایی که میتوانید از مردم حذر کنید. ۴- تغذیه خوب و سالم داشته باشید، مقادیر زیاد ویتامین C و D مصرف کنید. ۵- بسیار ورزش کنید. ۶- اگر توانستید حتما واکسن بزنید.
۱- ماسک ان-۹۵ بزنید، کرونا از ماسکهای معمولی رد میشود. ۲- فیلتر هوای قوی هپا بگذارید. ۳- تا جایی که میتوانید از مردم حذر کنید. ۴- تغذیه خوب و سالم داشته باشید، مقادیر زیاد ویتامین C و D مصرف کنید. ۵- بسیار ورزش کنید. ۶- اگر توانستید حتما واکسن بزنید.
Date: چهارشنبه, مارس 18, 2020 - 20:00
درباره نویسنده/هنرمند
 | دکتر حسن خاصهخان دانشآموخته ریاضیات بیولوژی و مُدلینگ از دانشگاه گوئلف انتاریوی کاناداست. وی در زمینه مُدلسازی ریاضی باکتریها تحقیقات گستردهای داشته و در انتاریو تدریس نیز نموده است. |
ویراستار اول: آرش مقدم؛ ویراستار نهایی: پر ابراهیمی - ویراستاری موقت: عباس حسنلو
ویراستار اول: آرش مقدم؛ ویراستار نهایی: پر ابراهیمی - ویراستاری موقت: عباس حسنلو

































